Coeficiente de Poisson
Ensanchamiento por efecto Poisson del plano
longitudinal medio de un prisma comprimido a lo largo
de su eje, el grado de ensanchamiento depende del
coeficiente de Poisson, en este caso se ha usado 

El coeficiente de Poisson (denotado mediante la letra griega 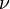 ) es unaconstante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
) es unaconstante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
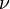 ) es unaconstante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
) es unaconstante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.Materiales isótropos [editar]
Si se toma un prisma mecánico fabricado en el
material cuyo coeficiente de Poisson
pretendemos medir y se somete este prisma a
una fuerza de tracción aplicada sobre sus
bases superior e inferior, el coeficiente de
Poisson se puede medir como: la razón entre
el alargamiento longitudinal producido
dividido por el acortamiento de una longitud
situada en un plano perpendicular a la
dirección de la carga aplicada. Este valor
coincide igualmente con el cociente de
deformaciones, de hecho la fórmula usual para
el Coeficiente de Poisson es:
material cuyo coeficiente de Poisson
pretendemos medir y se somete este prisma a
una fuerza de tracción aplicada sobre sus
bases superior e inferior, el coeficiente de
Poisson se puede medir como: la razón entre
el alargamiento longitudinal producido
dividido por el acortamiento de una longitud
situada en un plano perpendicular a la
dirección de la carga aplicada. Este valor
coincide igualmente con el cociente de
deformaciones, de hecho la fórmula usual para
el Coeficiente de Poisson es:
Donde ε es la deformación.
Para un material isótropo elástico
perfectamente incompresible, este es igual a 0,5. La mayor parte de los materiales prácticos en la ingeniería rondan entre 0,0 y 0,5, aunque existen algunos materiales compuestos llamados materiales augéticos que tienen coeficiente de Poisson negativo. Termodinámicamente puede probarse que todo material tiene coeficientes de Poisson en el intervalo (-1, 0,5), dado que la energía elástica de deformación (por unidad de volumen) para cualquier material isótropo alrededor del punto de equilibrio (estado natural) puede escribirse aproximadamente como:
La existencia de un mínimo relativo de la
energía para ese estado de equilibrio requiere:
energía para ese estado de equilibrio requiere:
Esta última condición sólo se puede cumplir si el coeficinete de Poisson cumple

Ley de Hooke generalizada [editar]
Conociendo lo anterior se puede concluir que
al deformarse un material en una dirección
producirá deformaciones sobre los demás
ejes, lo que a su vez producirá esfuerzos en
todos lo ejes. Por lo que es posible generalizar
la ley de Hooke como:
Materiales ortótropos [editar]
Para materiales ortotrópicos (como la madera), el cociente entre la deformación unitaria longitudinal y la deformación unitaria transversal depende de la dirección de estiramiento, puede comprobarse que para un material ortotrópico el coeficiente de Poisson aparente puede expresarse en función de los coeficientes de Poisson asociados a tres direcciones mutuamente perpendiculares. De hecho entre las 12 constantes elásticas habituales que definen el comportamiento de un material elástico ortotrópico, sólo 9 de ellas son independientes ya que deben cumplirse las restricciones entre los coeficientes de Poisson principales y los módulos de Young principales:
Valores para varios materiales [editar]
El coeficiente de Poisson es adimensional.
Para ver el valor del coeficiente de Poisson
para varios materiales consultar losvalores del
coeficiente de Poisson del Anexo:Constantes
elásticas de diferentes materiales.
Véase también [editar]
Referencias [editar]
Bibliografía [editar]
- Ortiz Berrocal, L., Elasticidad, McGraw-Hill, 1998, ISBN 84-481-2046-9.
Enlaces externos [editar]
- (Inglés) Materiales Augéticos
| |||||
| [ocultar]Fórmulas de conversión | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Los materiales elásticos lineales isótropos homogéneos tienen sus propiedades elásticas únicamente determinadas por dos módulos cualesquiera de los especificados anteriormente, por lo tanto, cualquier otro módulo de elasticidad puede ser calculado de acuerdo a estas fórmulas. | ||||||||||
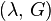 |  |  |  |  |  | 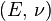 | 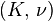 |  |  | |
 | 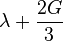 |  | 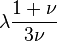 |  |  |  | ||||
 | 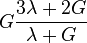 | 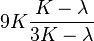 |  |  |  |  | 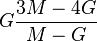 | |||
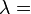 |  |  |  | 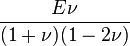 |  | 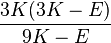 |  | |||
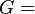 |  | 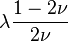 | 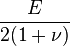 | 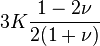 | 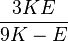 | |||||
 | 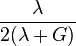 |  |  |  | 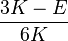 |  | ||||
 | 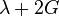 |  | 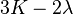 |  |  | 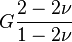 |  |  | 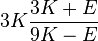 | |

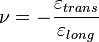


![\begin{cases}
\varepsilon_x = \cfrac {1}{E}
\left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] \\
\varepsilon_y = \cfrac {1}{E}
\left[ \sigma_y - \nu \left( \sigma_x + \sigma_z \right) \right] \\
\varepsilon_z = \cfrac {1}{E}
\left[ \sigma_z - \nu \left( \sigma_x + \sigma_y \right) \right] \end{cases}](http://upload.wikimedia.org/math/3/a/3/3a36ebb011815d396533edcbf118aafc.png)

 ) •
) •  ) •
) •  ) •
) •  ) •
) • ) •
) •  )
)
No comments:
Post a Comment